Jonathan Mann

Understanding Recursion in Haskell

To understand how recursion works, let’s walk through a simple example step by step. As a learning tool, we’ll create a simple function that raises the number two to a the power of whatever number is given as input. Let’s take a look at the implemenation to get a better idea of how the process works.

Implementation

Consider the following code :

r_two_to_power :: Int -> Integer
r_two_to_power 0 = 1
r_two_to_power n = r_two_to_power (n-1) + r_two_to_power (n-1)

Visualization

To get a clearer picture of what is going on, consider the diagram below: 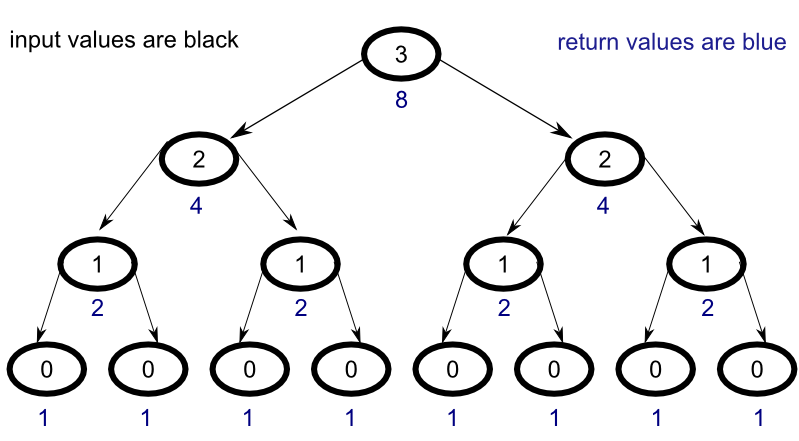With the exception of the nodes that satisfy the base case and return the value 1, each node has two child nodes. The return value of the parent node is the sum of the return values of its children. At the base of the pyramid, where each node receives the value of 0 as input satisfying the base case, the sum of the return values for the eight nodes is 8 since each node returns the value 1.

In the next level up, where each node has an input value of 1, the return value is sum of its child nodes, so each of the four nodes on this level has a return value of 2.

Similarly, in the subsequent level, where each node has an input value of 2, both of the nodes return 4.

Finally, at the top level, the node with an input value of 3 returns 8, the sum of its child nodes.

Interestingly, you can see that on each level, if you sum the return values for all the nodes, you always get back 8, the final return value for the problem.

Explanation

Let’s walk through the code line by line.

r_two_to_power :: Int -> Integer

The first line indicates that the function “r_two_to_power” will take in datatype Int and return the datatype Integer. The difference between these two datatypes has to do with the maximum size of the integer that the datatype can store. For our purposes, you can simply think of both types as integers, but a detailed explanation can be found here.

r_two_to_power 0 = 1

The second line establishes the base case. Whenever the value 0 is passed to the function, the value 1 is returned.

r_two_to_power n = r_two_to_power (n-1) + r_two_to_power (n-1)

The final line gives instructions for what the function should return for any number “n” not in the base case. Here the function calls itself recursively for the (n - 1) case until the base case is reached and adds the returned value to another instance of the (n - 1) case.

Example

As an example, let’s walk through what happens when we input the number 3 into the function. During the tracing process, we will skip the first line since it simply tells the function what to expect.

r_two_to_power 3

Since the input does not match the base case, the final line is evalutated:

r_two_to_power 3 = r_two_to_power (3-1) + r_two_to_power (3-1)

In order to find the solution, we must now resolve the following function:

r_two_to_power (3-1)

which is equivalent to

r_two_to_power 2

Following the same steps with an input of 2, we arrive at the following :

r_two_to_power 2 = r_two_to_power (2-1) + r_two_to_power (2-1)

Similarly, with an input of 1, we arrive at the following :

r_two_to_power 1 = r_two_to_power (1-1) + r_two_to_power (1-1)

Now we’re onto something though, because when we pass the input value 0 into our function, the base case is satisfied, and the function returns the value 1.

Now that we have gotten to the bottom of things, the solution can propagate back up the chain, but since this is a naive implementation, every recursive call must be evaluated all the way down to its base case (or one of its base cases if more than a single base case is defined) in order to return a value.